When we’re talking about major topics in secondary school math, we can’t leave out: Differentiation.
It is that giant topic that you can’t avoid in the exams, as there will surely be at least a few questions on differentiation. Whether you like it or not, how well you perform in math partly hinges on how confident you are in this topic. (Another big topic is trigonometry – check out our guide for that too!)
To help you in your revision, we’ve gathered the most essential points you need to know about differentiation, right here in this article.
Rules of differentiation
The only way to get over this big, scary-looking chapter is to look at it very systematically. Break it down into different skills and methods you need to master. That way, you can conquer them one by one, and spend more time on the ones you are unsure about.
The best way to master these rules is to focus on one at a time, building up your skills bank as you go along. For example, find practice questions that are purely on differentiation (no application, no word problems) so you can practice the rules.
Start easy! Make sure you master these basics before moving on to advanced differentiation questions that involve exponentials, logarithms, and trigonometry!
Rules for differentiation of trigonometric functions

Note: x is the angle in radians
Rules for differentiation of exponential and logarithmic functions

Must-know graph terminology for differentiation
- The tangent is a straight line that only intersects a curve at one point. It is used to approximate the gradient of the curve at that intersection point.
- The normal is the straight line perpendicular to the tangent, so its gradient is the negative reciprocal of that of the tangent.
- Parallel lines have the same gradient.
- When the tangent of a curve has a gradient of zero, it implies a stationary point on the curve.
- There are 3 types of stationary points, as shown below:

- If a function is ‘strictly increasing’, it means the gradient is positive (it could refer to only a range of values of x), that is,
- If a function is ‘strictly decreasing’, it means the gradient is negative (it could refer to only a range of values of x), that is,
How to solve common differentiation problems
Finding gradient of a function
- Differentiate function of the curve to find the gradient function.
- Substitute in the values of the point to find gradient of the tangent of that point.
- If you need to find the equation of the tangent, use the points and gradient to form the equation (recall: gradient-intercept form).
Determining the nature of stationary points
You can find any stationary points easily by first differentiating the function, then equating the first derivative to 0 (as the gradient at the stationary point must be zero). But, how would you know whether it is a maximum, minimum, or point of inflection? There are two tests you can use, as shown below.
a) First derivative test
- After differentiating the function, substitute in x values that are slightly before and after the stationary point.
- Check the signs of the first derivative at both points to determine the nature of the stationary point.
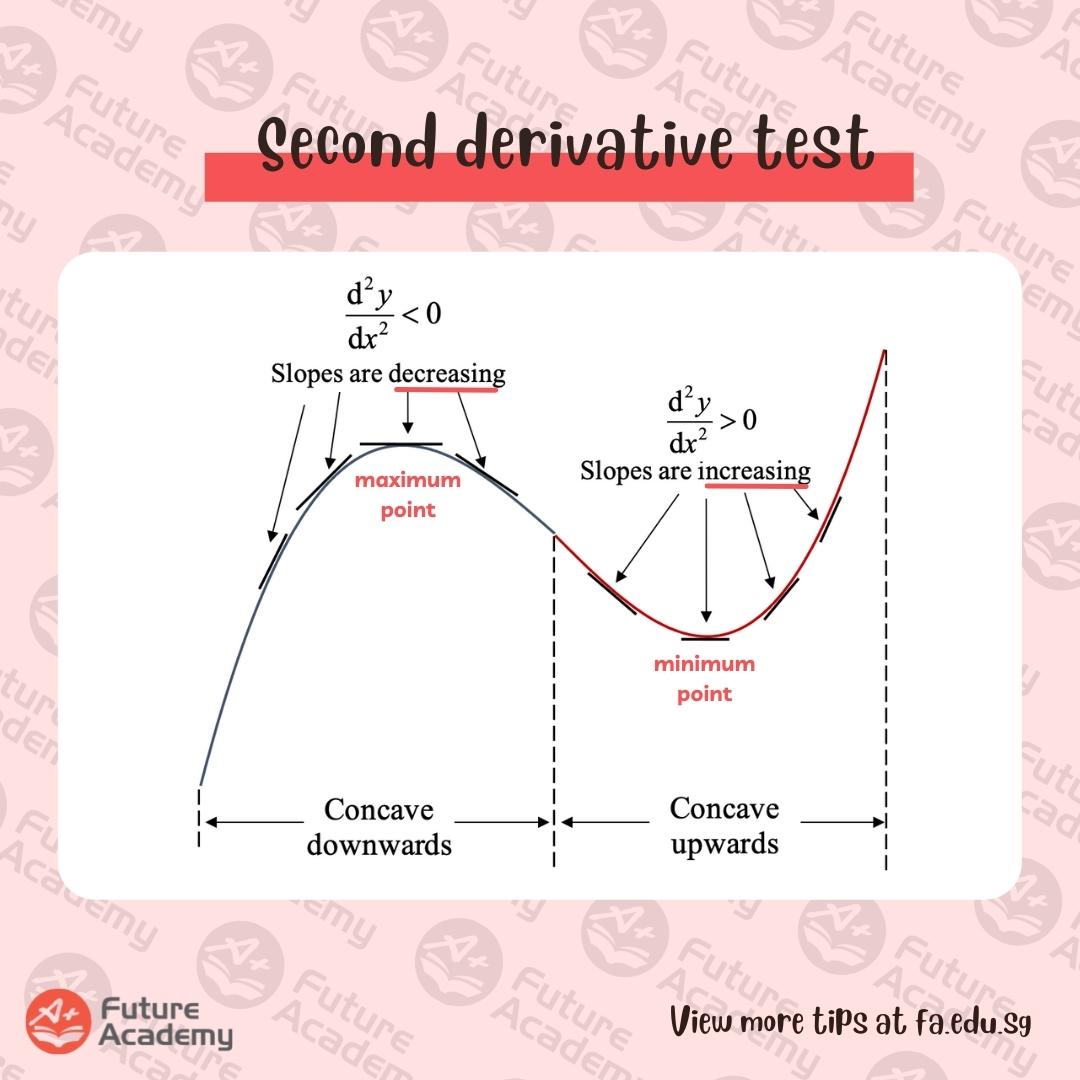
b) Second derivative test
- Differentiate the function, then differentiate the resulting function. This gives you the second derivative, which shows the rate of change of the gradient.
- Into the second derivative, substitute in the x value of the stationary point.
Real-life problems involving differentiation
The most common type of application question you will find in differentiation are those involving rate, maximum points, and minimum points. Some common question topics include:
- Travelling speed (kinematics)

- Rate of filling or emptying a water tank

- Variable perimeter/volume of a shape

Here are some tips for solving these types of application questions:
- Start by forming an equation.
Organise the information you have to create a function that links all the relevant unknowns together. To do this, you have to be familiar with how to calculate perimeters, area, and volume (including for shapes such as circle, cylinder, prism).
- Try to reduce the number of unknown variables you have
When you see p, q, and A all in one question, it can be intimidating. If your goal is to do , you can express q in terms of p to remove q from your equations.
- Be aware of physical limitations.
Now that you are solving a ‘real’ problem, make sure your answers make sense. For example, you may have 2 possible values for x, but if x is a measurement like a length, volume, or speed, it can’t be negative, so you have to eliminate the negative answer.
- Know what the question is asking for
Some students get so caught up trying to solve equations, they forget to directly answer the question. Are they asking for the rate, or “how much longer does it take to…”? Do you need to mention if the stationary points are maximum or minimum? Have they already given you an equation that you need to ‘show’? Also, take note of the required significant figures or decimal places the question requests for (if any), as well as the correct units.
Conclusion
Differentiation is a huge topic, but once you get the hang of it, solving the questions can even be fun! It’s okay if you can’t make sense of it just yet – practice makes perfect!
For personalised guidance and practice, our secondary math tutors can help you by providing you with organised worksheets and small group tutoring. There’s nothing to be shy about when asking for help!
Our IP Math tuition classes also go through more challenging questions like those found in IP school examinations, which will prepare you to tackle new and difficult questions. Get in touch with us now to schedule a class with us!



